One of the functions provided in the tools class is tools.estimate_rosette_leaf_count(). This implements a pre-trained convolutional neural network (which is accessible directly at networks.rosetteLeafRegressor()) to count the number of leaves on a rosette-type plant.
This guide reviews the basic process which was used to train the regression model to perform this leaf-counting task. It is intended to help users who wish to train their own models for similar tasks. The full code for this model appears in the models/leaf_counter_regressor.py source file.
Gathering the Training Data
The data used to train the leaf counter comes from the IPPN dataset of top-view arabidopsis rosette images. These images come with a CSV file called Leaf_counts.csv which provides the ground-truth number of leaves corresponding to each image.
Setting Up Model Parameters
Let's break down the setup of our model. See the documentation on model options for more information about these settings.
import deepplantphenomics as dpp
model = dpp.RegressionModel(debug=True, save_checkpoints=False, tensorboard_dir='/home/user/tensorlogs', report_rate=20)
These lines import the DPP library and start a new model for regression problems. We specify debug=True to see console output, save_checkpoints=False prevents the saving of checkpoints during training (it will still save the model at the end), and tensorboard_dir specifies the location to write Tensorboard accumulators so we can visualize the training process. report_rate=20 means that we will report results for one training batch and one testing batch every 20 batches.
# 3 channels for colour, 1 channel for greyscale
channels = 3
# Setup and hyperparameters
model.set_batch_size(4)
model.set_number_of_threads(8)
model.set_image_dimensions(128, 128, channels)
model.set_resize_images(True)
These lines tell us about the input images. In this case, we are going to use batches of 4 examples for each iteration of training (since this is a very small dataset). We are going to use 8 threads for each Tensorflow input producer. This is useful if a single producer thread can't keep up with the GPU. It normally doesn't matter, but we're training on a machine with a lot of cores so why not use them?
Since the size of images varies in this dataset, we are going to choose to resize them to 128x128. We could also choose to resize them by cropping or padding instead.
model.set_num_regression_outputs(1)
model.set_test_split(0.2)
model.set_validation_split(0.0)
model.set_learning_rate(0.0001)
model.set_weight_initializer('xavier')
model.set_maximum_training_epochs(500)
These are hyper-parameters to use for training. The first line specifies that we are doing a regression problem with one output: the number of leaves.
We are going to use 20% of the examples for testing and none of them for validation, meaning that 80% of the examples are used for training. We are not using any regularization. We will use an initial learning rate of 0.0001. We are going to initialize our layer weights using the Xavier (Glorot) initialization scheme.
We will train until 500 epochs - i.e. until we have seen all of the examples in the training set 500 times.
Repeatable Train/Test/Validation Splits
We want to ensure that the images are split the same way into training, testing, and validation sets between each successive run. This is important because we want to isolate the test data while we perform model selection on the trianing and validation data. If the data was re-shuffled, this would leak test data into our training and validation sets, and vice versa.
By default, DPP will save the train/test/validation split it generated the first time we train with a given dataset (in mask_ckpt.txt); it will then load that same split when reusing that dataset. This effect can be overridden so that a new split is generated every time a dataset is loaded and trained on. We do this by extending the model options above with the following:
model.force_split_shuffle(True)
Specifying Augmentation Options
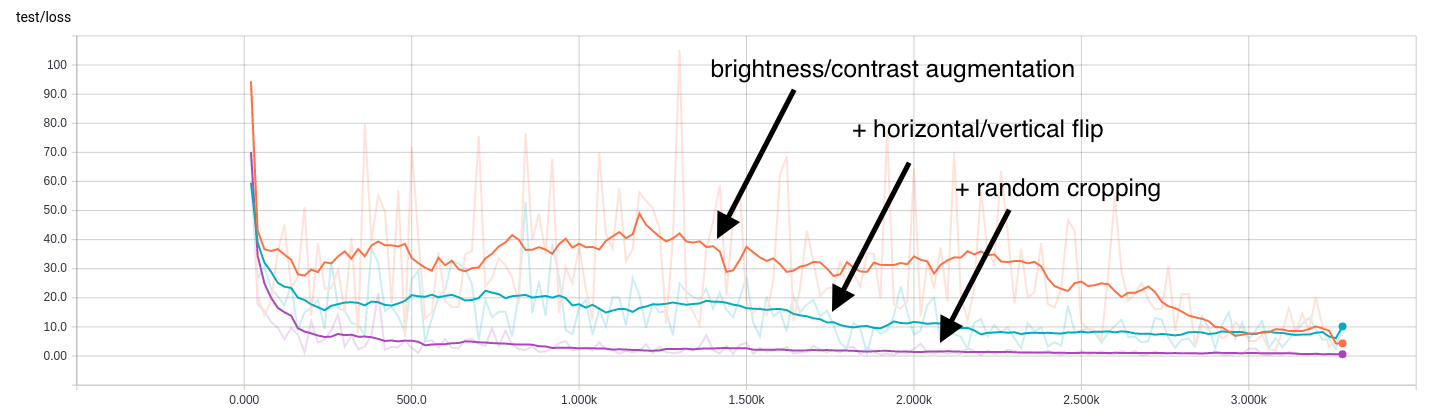
Since the size of the dataset is extremely small (165 images), it is necessary to use data augmentation. This means that we are going to artificially expand the size of the dataset by applying random distortions to some of the training images. The augmentations we are going to use are: randomly skewing the brightness and/or contrast, randomly flipping the images horizontally and/or vertically, and applying a random crop to the images.
The brightness/contrast augmentations are probably not needed as all of the images are taken under the same scene conditions, but it may help the trained network generalize to other datasets.
# Augmentation options
model.set_augmentation_brightness_and_contrast(True)
model.set_augmentation_flip_horizontal(True)
model.set_augmentation_flip_vertical(True)
model.set_augmentation_crop(True)
At test time, the images will be cropped to center in order to maintain the same input size. To illustrate the importance of data augmentation, here are test regression loss results showing the difference adding each augmentation makes:
Loading the Data
A function is included specifically for loading the data for this task.
# Load all data for IPPN leaf counting dataset
model.load_ippn_leaf_count_dataset_from_directory('./data/Ara2013-Canon')
For other tasks, your own images and labels can be loaded via loaders for directories and CSV files. For example, if you had your images in a directory called data and a CSV file data/my_labels.csv where the first column is the filename and the second column is the number of leaves, you could do this instead:
# ALTERNATIVELY - Load labels and images
model.load_multiple_labels_from_csv('./data/my_labels.csv', id_column=0)
model.load_images_with_ids_from_directory('./data')
Building the Network Architecture
We are going to use a small convolutional neural network for this task. It is comprised of four convolutional layers. There are no fully connected layers except the output layer. Each convolutional layer is followed by a pooling layer.
# Define a model architecture
model.add_input_layer()
model.add_convolutional_layer(filter_dimension=[5, 5, channels, 32], stride_length=1, activation_function='tanh')
model.add_pooling_layer(kernel_size=3, stride_length=2)
model.add_convolutional_layer(filter_dimension=[5, 5, 32, 64], stride_length=1, activation_function='tanh')
model.add_pooling_layer(kernel_size=3, stride_length=2)
model.add_convolutional_layer(filter_dimension=[3, 3, 64, 64], stride_length=1, activation_function='tanh')
model.add_pooling_layer(kernel_size=3, stride_length=2)
model.add_convolutional_layer(filter_dimension=[3, 3, 64, 64], stride_length=1, activation_function='tanh')
model.add_pooling_layer(kernel_size=3, stride_length=2)
model.add_output_layer()
Depending on your task, you may have better results with larger or smaller networks. Don't assume that a large model is better, especially with small datasets! Try a few different configurations with different feature extractors (the convolutional layers and accompanying machinery) and classifiers (the fully connected layers).
Training
We begin training the model by simply calling the training function.
# Begin training the regression model
model.begin_training()
The model will train until 500 epochs. We will see updates both in the console as well as in Tensorboard. At the end, loss statistics will be reported for the entire test set.
09:40AM: Results for batch 32980 (epoch 499) - Loss: 0.19386, samples/sec: 871.05
09:40AM: Stopping due to maximum epochs
09:40AM: Saving parameters...
09:40AM: Computing total test accuracy/regression loss...
09:40AM: Mean loss: -0.0272586610582
09:40AM: Loss standard deviation: 0.624978633174
09:40AM: Mean absolute loss: 0.480917639203
09:40AM: Absolute loss standard deviation: 0.400074431613
09:40AM: Min error: -1.19493865967
09:40AM: Max error: 1.5458946228
09:40AM: MSE: 0.391341326526
09:40AM: R^2: 0.904088812561
09:40AM: All test labels:
09:40AM: [ 9. 6. 6. 7. 9. 7. 10. 7. 9. 7. 9. 8. 11. 8. 9.
10. 13. 8. 9. 11. 13. 10. 11. 13. 7. 7. 8. 8. 6. 7.
6. 7. 9. 6. 6. 7.]
09:40AM: All predictions:
09:40AM: [ 8.1905098 6.8377347 6.05786324 6.85530901 9.53642273
6.90101051 9.07618999 7.18060684 9.11283112 7.32292271
10.06754875 9.54589462 10.39970398 8.09113407 8.87572861
9.58766937 11.90369415 7.8541441 8.67022324 11.41111469
11.82732868 10.79200935 11.04158878 11.80506134 6.51270151
7.24674559 7.92943382 8.56169319 5.93615294 6.48214674
6.16266203 7.30149126 8.1905098 6.8377347 6.05786324
6.85530901]
09:40AM: Histogram of L2 losses:
09:40AM: [2 0 0 1 0 0 0 0 0 1 0 0 0 0 2 0 0 0 0 0 0 1 0 0 1 1 0 0 1 0 0 1 0 0 0 0 0
0 3 2 0 2 0 0 0 3 1 1 0 1 1 0 1 0 1 1 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0
2 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1]
09:40AM: Shutdown requested, ending session...
For regression problems, the loss value is the L2 norm of the ground truth label subtracted from the regression output. This means that for a one-dimensional output, like leaf count, we can interpret the loss as the absolute difference in count.
Also, for one-dimensional output, notice that the L2 norm is reported as the "absolute" loss, while the relative difference is also reported. This is useful in cases (such as leaf counting) where we are interested in over- and under-prediction. For multi-dimensional outputs, the mean/std and absolute mean/std will be identical, since the L2 norm is never negative.
An error histogram is output as a vector of frequencies for 100 bins. Note that the min and max loss are also reported. The first bin corresponds to the interval (-inf, min] and the last bin corresponds to the interval [max, inf). The area between these bins is divided into 98 bins of equal size.
MSE (mean squared error) and R squared are also provided. For smaller test sets, the whole set of ground truth and predicted values are provided so that you can calculate whatever other statistics you need.
My Model's Not Converging, What Can I Do?
This model seems to do quite well on this task, as you can see the loss rapidly decreasing until it settles around a particular value. In other cases, your model may thrash around, never improving.
There are a few things you can try to encourage convergence.
- Lower the learning rate by an order of magnitude.
- Tune DropOut rates, or remove DropOut layers.
- Try a larger model. It may not have enough representational capacity for the problem.